Efficient second-harmonic generation of a femtosecond laser pulse in a LBO crystal
We demonstrate the highest efficiency (∼80%) second harmonic generation of joule level, 27 fs, high-contrast pulses in a type-I LBO crystal (lithium triborate). In comparison, nonlinear crystal (KDP crystal) gives a maximum efficiency of 26%. LBO thus offers high-intensity (>1018−19 W/cm2), ultra-high contrast femtosecond pulses,which have great potential for high energy density science and applications, particularly with nanostructured targets.
Intense, femtosecond laser pulse interaction with solids facilitates high energy density science and provides high brightness,ultrafast x-ray and terahertz sources on the one hand and energetic pulsed electron, proton, ion, and positron sources on the other—all on a tabletop. The advantage of such pulses is the “instantaneous” excitation of solid density matter,unlike studies with longer pulses where the excitation occurs over a partially ionized, expanding, lower than solid density plasma. In practice, an amplified femtosecond pulse has a longer picosecond wing sitting on a nanosecond pedestal and a femtosecond replica a few nanoseconds before.
Picosecond pedestals are typically suppressed by fast saturable absorbers , cross-wave polarization gating, theseeding of the amplifiers at high energy, or the improvement of compressor components. The first two involve nonlinear optical processes. In laser systems with intrinsic low contrast, external plasma mirroring and harmonic generation can improve the contrast. Second harmonic generation (SHG) is particularly attractive, since it is simple, robust, and easy to control. In practice, SHG is dependent on the availability of efficient, large crystals (for large amplified beams) with manageable dispersion and a high damage threshold. Therefore, there have been very few studies on this topic, particularly at high intensities
In this Letter, we demonstrate SHG of 800 nm, high contrast (109), and 27 femtosecond pulses at nearly 80% efficiency in a lithium triborate (LBO) crystal at intensities as large as 1400 GW/cm2. The resulting 400 nm, ultra-high contrast pulses can generate focused intensities of 1018−19 W/cm2 (considering focal waist to be 10 µm). We compare the LBO results to those from potassium KDP crystal (dihydrogen phosphate) under similar conditions and with other previous studies. We present numerical simulations for LBO that reproduce our results.

Fig. 1. (a) Schematic of the experimental setup (M1-M2, dichroic mirrors for 400 nm; BS beamsplitter; BD1–BD2, beam dumps), (b) pulse-width (measured using SPIDER), (c) bandwidth of fundamental 800 nm pulse, (d) intensity contrast (measured using SEQUIOA), and (e) crystal characteristics. SPIDER – spectral phase interferometry for direct electric field reconstruction (Amplitude Technologies); SEQUIOA (Amplitude Technologies) – a third-order cross correlator.
The experiment [Fig. 1(a)] was conducted inside a vacuum chamber (10−6 torr) using a chirped pulse amplified 150 TW Ti:sapphire laser system delivering 800 nm, 27 fs, and 50 nm bandwidth pulses at a 5 Hz repetition rate, with a beam diameter of 80 mm (Fig. 1). The laser was well stabilized (<± 5%) before data were taken. A type-I LBO crystal (Cristal Laser; 70 mm clear aperture, 2 mm thick, anti-reflection coated for both 800 nm and 400 nm) was used for SHG. Two mirrors coated for 400 nm (R > 99.9%) were placed after the LBO to eliminate residual fundamental radiation (800 nm). A pyroelectric detector (OPHIR PE100BF-DIF-C) measured the SHG energy. The spectrum of the second harmonic (SH) was measured by a single-shot spectrometer using a beamsplitter that picked off a small fraction (1%) of the SH beam through a fused silica window of the chamber. Similar measurements were obtained for a type-I KDP crystal (52 mm aperture and 1 mm thick; no anti-reflection coating). The crystals were rotated (both θ and φ) to get the highest signal, at the best phase-matching conditions. Crystal characteristics are presented in Fig. 1(e).
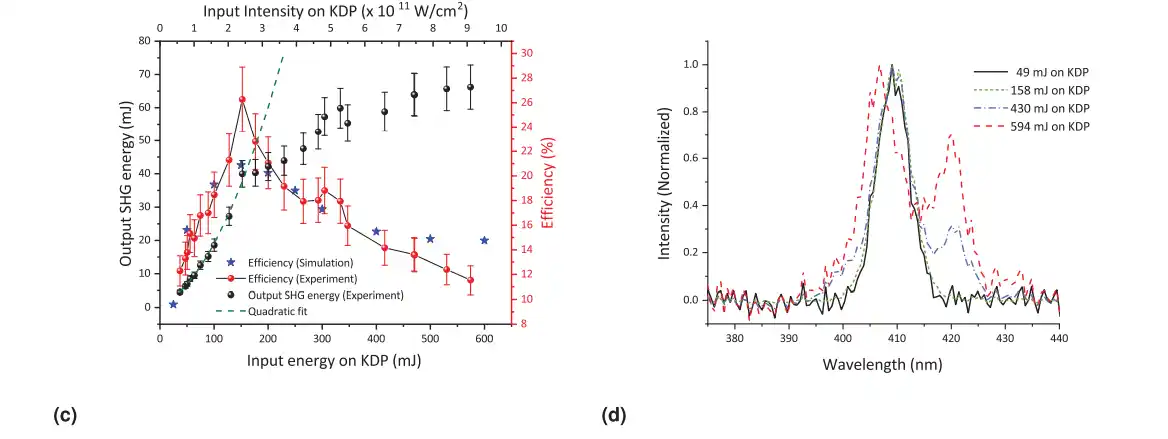
Fig. 2. (a) SHG efficiency from LBO crystal, (b) SHG spectrum of LBO crystal with varying input laser energy, (c) SHG efficiency from KDP crystal, (d) SHG spectrum of KDP crystal with varying input laser energy. (The error bars in the data are set by repeated measurements. Each point is an average over 10 pulses.)
Figure 2(a) shows the SHG energy and conversion efficiency as a function of both input energy and input intensity on the LBO. At lower intensities, the SHG process has an output that scales as the square of the input energy, as seen from the quadratic fit. At high intensities used in the experiment, however, the output energy is seen to deviate slightly from the quadratic behavior into saturation (at ∼80%). The simulation matches the experiment quite well up to an input energy of 500 mJ, though saturation sets in at a lower value (at 70%) than in the experiment. KDP shows similar behavior [Fig. 2(c)] at low energies, reaching a maximum of around 26% at 150 mJ (an intensity of ∼250 GW/cm2) before falling off at high intensities The deviation from the quadratic behavior is seen to be much more, attributable to KDP having an order of magnitude higher χ (3) value than LBO. The saturation or falloff is expected from significant coupling to higher-order nonlinearities. The marginal deviation from the experimental curves can be attributed to the assumption of perfectly Gaussian pulses in space and time in simulations and not accounting for the initial pulse phase modulations. The LBO efficiency reaches an attractive 50% at energies as low as 400 mJ and a peak of about 80% at 1.2 J. We believe such conversion efficiencies for highintensity, sub-100 femtosecond pulses have not been measured in other studies and hence are really promising for the field of high energy density physics. We see much larger efficiencies for the LBO than for KDP. LBO has a superior damage threshold,higher nonlinearity, a smaller walk off angle, and a larger acceptance angle as compared to KDP, which could explain the differences. Also, the nonlinear refractive index n2 for KDP (∼1.4 × 10−15 cm2/W) is an order of magnitude higher than LBO (∼2.1 × 10−16 cm2/W). This leads to stronger thirdorder effects in KDP in the intensity range of our experiments.This stronger third-order nonlinearity can adversely affect the SHG via beam reshaping and phase mismatch, thereby limiting the conversion and causing a reduction in efficiency beyond a certain intensity range. The lower damage threshold of the KDP crystal also makes it difficult to use at higher intensities.
Figure 2(b) shows the spectra of SH pulses from LBO for different input energies. We note that the bandwidth of the spectra increases with input energy and the spectra develop additional modulations, which are known to arise from higherorder nonlinearities like self-phase modulation . At lower input energy, the bandwidth is about 6 nm and at higher input energy, about 9 nm. The higher bandwidth implies that the SH pulse generated at higher intensities could potentially be compressed to lower pulse durations. Present simulations indicatethe SH pulse duration to be about 65 fs, consistent with our preliminary measurements using a self-diffraction frequencyresolved optical gating (SD FROG; Fig. S1 in Supplement 1). Figure 2(d) shows SH spectra from the KDP crystal for different input intensities. Here again the SH spectra are broadened and modulated with the increase in energy. Let us compare our results to earlier reports (Table 1). First, we used the highest femtosecond pulse intensity so far. Our pulse bandwidth is the highest and, hence, we face the most adverse effects of walkoff and possible interference of higher-order nonlinearities, given that our intensities reach 1400 GW/cm2. Nevertheless, it is gratifying to note that we have reached conversion efficiencies as large as 80%. This is extremely encouraging for applications particularly in high energy density science where the whole purpose of the SHG is the improvement in the intensity contrast of the pulses. Among other results, the largest efficiencies reported were by Hillier et al. at 75% and Aoyama et al. at 80%. Hillier et al. used 500 fs pulses at much larger input energies, but also much larger crystal sizes, keeping the intensity on the crystal rather low (250 GW/cm2 ). Note that their pulses had a bandwidth of only about 3 nm and thus much less walkoff; hence, they were able to use larger crystal lengths. Similarly, Aoyama et. al used 100 fs pulses with a bandwidth of about 10 nm and intensity on the crystal around 192 GW/cm2 – i.e., a longer pulse duration and shorter bandwidth than in our experiment. Second, in the regime of pulse energies used in our experiments, the higher-order effects (especially self-phase modulation) induce a weak spectral broadening and do not strongly affect the conversion efficiency. It may, however, have implications for the SH pulse duration. Preliminary measurements using SD FROG indicate a pulse duration of about 60 fs, in good agreement with simulations (65 fs; Fig. S1 in Supplement 1). Third, the contrast of the SH pulse is not measurable with the current technology. We can, however, estimate the best value to be the square of the contrast of the input pulse, the latter being 109 in our case. In practice, it may not be exactly the best achievable, but we can estimate an improvement in the picosecond contrast to be at least a million fold . Fourth, our input pulses are p-polarized and the SH pulses are s -polarized, measured using an analyzer/polarizer setup.

Table 1. Comparison of SHG Conversion from Different Experiments.
Finally, we consider the role of self-focusing on the SH beam quality. The B-integral for the pump beam is between 0.5-1 π in our experiment, which is below the value for small-scale self-focusing (SSSF) to be significant. Given the beam divergence, the B-integral is likely to be smaller than this value. The beam profiles were reasonably smooth, and no damage or gray tracking was observed, even after many runs of the experiment (Fig. S2 in Supplement 1). For SSSF, we evaluate from the Bespalov–Talanov theory the lower bound for the growth length for modulational instability developing on a flat beam profile with the highest intensity from our experiments I = 1.4 TW/cm2 : Lg = λI /Pcr ∼ 0.2 mm, where Lg is the growth length and Pcr is the critical power for self-focusing. This ength is smaller than the crystal length, leading to the possibility of observing modulational instability. However, the latter needs several Lg to grow significantly (assuming the high intensity to be preserved along the path), and we did not observe damage of the crystal. Hence, it is likely that our highest intensities were below or close to the threshold. We report a high (∼80%) SHG efficiency from a 2 mm thick LBO crystal using 800 nm, 27 femtosecond and 50 nm bandwidth, 109 intensity contrast pulses. In comparison, we get only 26% from a 1 mm KDP crystal. Efficient SHG of such high bandwidth pulses requires proper consideration of walkoff, which adds more appeal to this result. We show SHG spectral broadening at high intensities, indicating the effects of higher-order nonlinearities. We also present numerical simulations which match the experimental data fairly well and help us understand the physical process better. Owing to such high efficiencies, we are able to reach intensities 1018−19 W/cm2 when focused on a target. In addition, SHG can improve the intensity contrast by many orders of magnitude; hence, these pulses can facilitate clean femtosecond experiments with structured targets to produce hot, dense plasma conditions and ultrabright radiation sources.
1. D. Hillier, C. Danson, S. Duffield, D. Egan, S. Elsmere, M. Girling, E.Harvey, N. Hopps, M. Norman, S. Parker, P. Treadwell, D. Winter, and T. Bett, Appl. Opt. 52, 4258 (2013).
2. M. Hornung, G. A. Becker, A. Seidel, J. Reislöhner, H. Liebetrau, L. Bock, S. Keppler, A. Kessler, M. Zepf, J. Hein, and M. C. Kaluza, Appl. Sci. 5, 1970 (2015).
3. M. Aoyama, T. Harimoto, J. Ma, Y. Akahane, and K. Yamakawa, Opt. Express 9, 579 (2001).
4. K. Mori, Y. Tamaki, M. Obara, and K. Midorikawa, J. Appl. Phys. 83, 2915 (1998).
5. A. Marcinkevicius, R. Tommasini, G. Tsakiris, K. Witte, E. Gaižauskas, ˇand U. Teubner, Appl. Phys. B 79, 547 (2004).
6. I. A. Begishev, M. Kalashnikov, V. Karpov, P. Nickles, H. Schönnagel, I. A. Kulagin, and T. Usmanov, J. Opt. Soc. Am. B 21, 318 (2004).
7. S. Y. Mironov, V. N. Ginzburg, V. V. Lozhkarev, G. A. Luchinin, A. V. Kirsanov, I. V. Yakovlev, E. A. Khazanov, and A. A. Shaykin, Quantum Electron. 41, 963 (2011).















